ΠΑΡΑΤΗΡΗΣΕΙΣ
Ο χρόνος για μία πλήρη περιστροφή του σημείου P πάνω στον κύκλο, είναι ίσος με την περίοδο της κίνησης.
Η γωνιακή ταχύτητα του σημείου P είναι ίδια με τη γωνιακή συχνότητα, ω, της απλής αρμονικής κίνησης.
Η αρχική φάση, δ, των απλών αρμονικών κινήσεων αντιστοιχεί στις γωνίες φ και θ τις οποίες σχηματίζει το OP με τους άξονες x και y, αντίστοιχα.
Η ακτίνα R του κύκλου είναι ίση με το πλάτος της απλής αρμονικής κίνησης.
Αν υψώσουμε στο τετράγωνο τις σχέσεις:
και προσθέσουμε κατά μέλη, θα έχουμε:
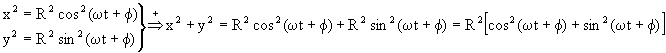
Δηλαδή η εξίσωση κίνησης θα είναι:
![]()
Η τελευταία μορφή της εξίσωσης κίνησης είναι αυτή που φαίνεται πάνω αριστερά στο παράθυρο του πειράματος.
Εάν, τώρα, δεν είχαμε κυκλική κίνηση αλλά ελλειπτική, δηλαδή αντί για ακτίνα R είχαμε άξονες α και β, θα είχαμε εξίσωση της μορφής:
Εξετάστε και αυτή την περίπτωση όταν θα κάνετε το πείραμα!
ΥΠΟΛΟΓΙΣΜΟΣ ΤΑΧΥΤΗΤΑΣ
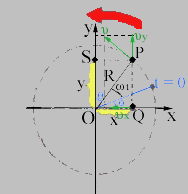 |
Η γραμμική ταχύτητα ενός σώματος που
εκτελεί κυκλική κίνηση δίνεται από τη σχέση:
Από τη γεωμετρία του σχήματος προκύπτει ότι: υx = - ωR sin(ωt + φ) και υy = - ωR sin(ωt + θ).
|
Οι ταχύτητες των σημείων Q και S βρίσκονται με παραγώγιση της θέσης ως προς το χρόνο. Εφόσον
| x = R cos(ωt + φ) |
| y = R cos(ωt + θ) |
εύκολα προκύπτει ότι:
| υx = - ωR sin(ωt + φ) |
| υy = - ωR sin(ωt + θ) |
ΥΠΟΛΟΓΙΣΜΟΣ ΕΠΙΤΑΧΥΝΣΗΣ
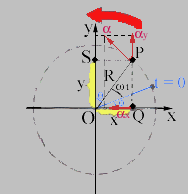 |
Η επιτάχυνση του σημείου P δίνεται από τη
σχέση:
και κατευθύνεται ακτινικά προς το σημείο Ο. Από τη γεωμετρία του σχήματος προκύπτει ότι: αx = - ω2R cos(ωt + φ) και αy = - ω2R cos(ωt + θ).
|
Οι ταχύτητες των σημείων Q και S βρίσκονται με παραγώγιση της ταχύτητας ως προς το χρόνο (ή με δεύτερη παραγώγιση της θέσης ως προς το χρόνο). Εφόσον
| υx = - ωR sin(ωt + φ) |
| υy = - ωR sin(ωt + θ) |
εύκολα προκύπτει ότι:
| αx = - ω2R cos(ωt + φ) |
| αy = - ω2R cos(ωt + θ) |