ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΚΑΙ ΟΜΑΛΗ
ΚΥΚΛΙΚΗ ΚΙΝΗΣΗ
- Η ομαλή κυκλική κίνηση σχετίζεται με την
απλή αρμονική κίνηση. Το πως, θα το
δούμε ευθύς αμέσως!
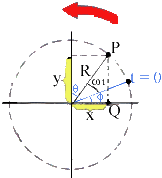 |
Θεωρούμε το σημείο P, το οποίο
εκτελεί ομαλή κυκλική κίνηση (δηλαδή
έχει σταθερή γωνιακή ταχύτητα, ω) πάνω
σε κύκλο ακτίνας R, και τις προβολές
του P, Q και S πάνω στους άξονες x και y,
αντίστοιχα.
Έστω ότι τη χρονική στιγμή t = 0 το
διάνυσμα θέσης (OP) σχηματίζει γωνίες φ
και θ με τους άξονες x και y, αντίστοιχα.
Σε κάποια τυχαία χρονική στιγμή το
διάνυσμα θέσης (OP) θα σχηματίζει
γωνίες ωt + φ και ωt + θ με τους άξονες x
και y, αντίστοιχα Δηλαδή, καθώς το σώμα
περιστρέφεται πάνω στον κύκλο, οι
γωνίες που σχηματίζει με τους άξονες x
και y μεταβάλλονται συναρτήσει του
χρόνου. |
Επί πλέον, οι προβολές Q και S κινούνται
παλινδρομικά πάνω στις διαμέτρους του
κύκλου οι οποίες είναι παράλληλες στους
άξονες x και y, ανάμεσα στα όρια ± R. Όπως
είναι προφανές και από το σχήμα, το σημείο P
και οι προβολές Q και S έχουν τις ίδιες
συντεταγμένες x και y, αντίστοιχα. Από τα
ορθογώνια τρίγωνα OPQ και OPS βλέπουμε ότι οι
συντεταγμένες x και y δίνονται από τις
σχέσεις:
| x = R cos(ωt + φ) |
| y = R cos(ωt + θ) |
|
ή |
| y = Rsin(ωt + φ) |
Επομένως καταλήγουμε στο συμπέρασμα ότι
οι παλινδρομικές κινήσεις των Q και S πάνω
στους άξονες x και y, αντίστοιχα, δεν είναι
παρά απλές αρμονικές κινήσεις. Γενικότερα,
προκύπτει το συμπέρασμα ότι: Η προβολή
ενός σημείου το οποίο εκτελεί ομαλή κυκλική
κίνηση πάνω σε μία διάμετρο εκτελεί απλή
αρμονική κίνηση πάνω στη διάμετρο αυτή.
Από τις παραπάνω εξισώσεις προκύπτει και
η εξίσωση
κίνησης.
Έτσι συμπεραίνουμε ότι η ομαλή κυκλική
κίνηση μπορεί ν' αναλυθεί σε δύο απλές
αρμονικές κινήσεις πάνω σε δύο κάθετους
άξονες με σχετική διαφορά φάσης 900.
Από τα παραπάνω, προκύπτουν
κάποιες πολύ χρήσιμες παρατηρήσεις:
ΠΕΡΙΣΣΟΤΕΡΑ...
Εάν θέλετε να δείτε περισσότερα
σχετικά με την απλή αρμονική κίνηση πατήστε
ΕΔΩ.
Δείτε το σχετικό
εικονικό πείραμα
