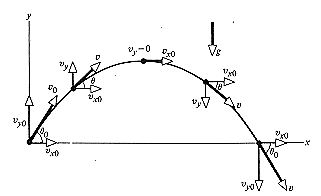
Η πλάγια βολή είναι αποτέλεσμα της υπέρθεσης δύο κινήσεων:
της κίνησης ενός σώματος, σε κατακόρυφη διεύθυνση, που πέφτει ελεύθερα με σταθερή επιτάχυνση (επιτάχυνση της βαρύτητας)
της ισοταχούς κίνησης σε οριζόντια διεύθυνση.
Προκειμένου να μελετήσουμε αυτή την κίνηση, συνήθως, αγνοούμε την επίδραση που ασκεί η αντίσταση του αέρα.
Επιλέγουμε ένα σύστημα αναφοράς..

Έστω ότι η θετική κατεύθυνση y είναι προς τα πάνω. Τότε:
|
(όπως είναι και στη μονοδιάστατη ελεύθερη πτώση) |
|
| (έχουμε αγνοήσει την τριβή του αέρα). |
Υποθέτουμε ότι το βλήμα εκτοξεύεται από την αρχή των συντεταγμένων (x0 , y0 ), τη χρονική στιγμή t=0 με κάποια αρχική ταχύτητα υ0 η οποία σχηματίζει γωνία θ0 με τον άξονα των x..Από τριγωνομετρία ισχύουν:
![]()
Έτσι, οι x και y συνιστώσες της
αρχικής ταχύτητας θα είναι:
Όμως, 
Στην περίπτωσή μας, λοιπόν οι συνιστώσες της ταχύτητας και οι συντεταγμένες της κίνησης για κάθε χρονική στιγμή είναι:
|
|
Όπως φαίνεται από τις παραπάνω εξισώσεις, η υx είναι σταθερή, σε όλες τις χρονικές στιγμές, και ίση με τη x συνιστώσα της αρχικής ταχύτητας. Αυτό συμβαίνει επειδή δεν έχουμε οριζόντια συνιστώσα της επιτάχυνσης. Επίσης, η υy και η y είναι οι σχέσεις που περιγράφουν την ελεύθερη πτώση.
Εάν λύσουμε την εξίσωση της x συνιστώσας, ως προς το χρόνο, και την αντικαταστήσουμε στην εξίσωση της y συνιστώσας, προκύπτει:

Η εξίσωση αυτή ισχύει για γωνίες
![]()
και είναι της μορφής
![]()
η οποία είναι εξίσωση παραβολής που διέρχεται από την αρχή των αξόνων.
Δηλαδή, η πλάγια βολή έχει παραβολική
τροχιά η οποία ορίζεται πλήρως εάν γνωρίζουμε τα
![]()
Το διάνυσμα της ταχύτητας του σώματος έχει μέτρο:
![]()
και η διεύθυνσή του δίνεται από τη σχέση
![]()
επειδή γνωρίζουμε ότι κάθε χρονική στιγμή είναι εφαπτομενικό στην τροχιά.
Μέγιστο ύψος βολής, ολικός χρόνος κίνησης και βεληνεκές
Για να βρούμε το μέγιστο ύψος θα χρησιμοποιήσουμε ότι, στην κορυφή της τροχιάς υy =0. Έτσι,
![]()
Επομένως,

Για να βρούμε τον ολικό χρόνο κίνησης, θα χρησιμοποιήσουμε ότι όταν το σώμα φτάνει στο έδαφος, y=0. Έτσι:

Για να βρούμε το βεληνεκές θ' αντικαταστήσουμε στην εξίσωση του διαστήματος στον άξονα x τον ολικό χρόνο. Οπότε
![]()
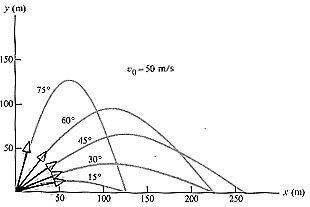
Όπως είναι προφανές το βεληνεκές, ![]() ,
γίνεται μέγιστο, όταν sin2θ0 =0, δηλαδή
,
γίνεται μέγιστο, όταν sin2θ0 =0, δηλαδή
![]()
Επομένως, για γωνία 45 έχουμε
μέγιστο βεληνεκές:![]()
Ακόμη, δύο συμπληρωματικές γωνίες έχουν ίδιο βεληνεκές. Βέβαια, δεν έχουν το ίδιο μέγιστο ύψος και τον ίδιο χρόνο κίνησης, όπως φαίνεται και από το σχήμα