Formation of Vortices in First Order Phase Transitions

Relevant Talk:          Physics of Solitons

Authors:   Alejandra Melfo and Leandros Perivolaropoulos

Abstract:
Using a toy model Lagrangian we investigate the formation of vortices in first order phase transitions. The evolution and interactions of vacuum bubbles are also studied using both analytical approximations and a numerical simulation of scalar field dynamics. A long lived bubble wall bound state is discovered and its existence is justified by using a simplified potential for the bubble wall interaction. The conditions that need to be satisfied for vortex formation by bubble collisions are also studied with particular emphasis placed on geometrical considerations. These conditions are then implemented in a Monte Carlo simulation for the study of the probability of defect formation. It is shown that the probability of vortex formation by collision of relativistically expanding bubbles gets reduced by about 10% due to the above mentioned geometric effects.

Work available in print:  PDF file of paper

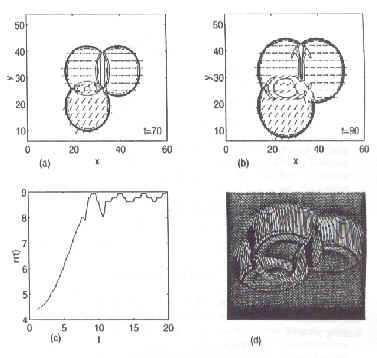
Numerical Simulations of Vortex Formation (Evolution of Scalar Field Magnitude (with minus sign)).

Bubble Walls Merging.   Large Phase Difference Between Bubbles (1.5MB).

(Click on the figures to view a simulation of two bubbles merging.  Notice the Delayed Merging of the Bubbles due to large phase difference)

Vortex Formation from Merging Bubbles  (1.5MB)

(Click on the figures to view the simulation)