Νευτώνια
Μηχανική
Ο
πρώτος Νόμος
του Νεύτωνα ορίζει
μια κλάση
συστημάτων
αναφορας: τα
αδρανειακά
συστήματα. Τα
αδρανειακά
συστήματα
είναι
συστήματα
αναφοράς για τα
οποία οι
τροχιές χωρίς
την παρουσία
δυνάμεων είναι
λύσεις της
εξίσωσης
dr/dt=0. Σε
αδρανειακά
συστήματα ο
δεύτερος Νόμος
του Νεύτωνα έχει την μορφή
F=dp/dt.
(r
=
συντεταγμένη,
F
= δύναμη,
p
= ορμή)
Έστω
Fik η δύναμη που
ασκεί το
σωμάτιο i
στο
σωμάτιο k. Ο τρίτος Νόμος
του Νεύτωνα λέει
ότι Fik=-Fki.
Οι
νόμοι του
Νεύτωνα είναι
κατάλληλοι για
την μελέτη
μηχανικων
συστημάτων που
δεν υποκεινται
σε
περιορισμούς (δεσμούς).
Οι
δεσμοί,
όπως
η απαίτηση για
σωμάτιο να
ακολουθει
σσυγκεκριμένη
καμπύλη στο
χώρο, μας
λένε ότι
υπάρχουν
εξωτερικές
δυνάμεις αλλα
δεν μας
καθορίζουν
ποιες είναι
αυτές οι
δυνάμεις.
Οι
δυνάμεις αυτές
είναι γνωστές
μόνο αναφορικά
με τα
αποτελέσματα
τους στην
κίνηση.
Οι
νόμοι
διατήρησης είναι
πολύ
σημαντικοί
στην λύση
προβλημάτων
μηχανικής.
|
|
Για
ένα σύστημα
σωματιδίων η
ορμή
διατηρείται αν Fext=0; Fext=0
Û P=constant.
|
|
|
Η στροφορμή (Μ)
διατηρείται
αν η
ροπή
text=0; text=0
Û Μ=σταθερή.
|
|
|
Η ενέργεια E=T+U
διατηρείται
αν
όλες οι
δυνάμεις
είναι
συντηρητικές; òF× dr=0
Û T+U=σταθερή.
|
Λαγκρανζιανή
Μηχανική
Έστω
ότι έχουμε ένα
σύστημα με
ολόνομους
δεσμούς. Ολόνομοι
δεσμοί είναι
δεσμοί της
μορφής
f(r1,r2,r3,¼,t)=0.
Μειώνουν
τον αριθμό των
βαθμών
ελευθερίας
ενός
συστήματος.
Αν οι
δεσμοί είναι
ολόνομοι τότε
οι δυνάμεις των
δεσμών δεν
εκτελούν δυνατό
έργο. Υποθέστε
ότι το σύστημα
έχει n
ανεξάρτητες
γενικευμένες
συντεταγμένες
{qi}. Υποθέστε
ακόμα ότι οι γενικευμένες
εφαρμοζόμενες
δυνάμεις
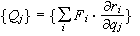
δίνονται
από τις σχέσεις
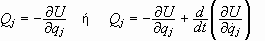
όπου
U βαθμωτή
συνάρτηση, δηλαδή
οι
γενικευμένες
εφαρμοζόμενες
δυνάμεις
προκύπτουν από
δυναμικό. Τότε
οι εξισώσεις
κίνησης
προκύπτουν από
τις εξισώσεις
Lagrange,
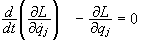 ,
,
όπου
L=T-U
είναι
η Lagrangian
του
συστήματος. L είναι
συνάρτηση των
συντεταγμένων
και των
ταχυτήτων.
Ορίζουμε
την γενκευμένη
ορμή ή συζηγή
ορμή ή
κανονική
ορμή
μέσω
της σχέσης
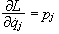 .
.
Αν η
Lagrangian δεν περιέχει
συγκεκριμένη
συντεταγμένη
qj
τότε
η συντεταγμένη
ονομάζεται
κυκλική
κυκλική
και η
αντίστοιχη
συζηγής ορμή
pj
διατηρείται.
Η
Hamiltonian
H ενός
συστήματος
δίνεται απο
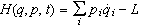 .
.
H
είναι
συνάρτηση των
γενικευμένων
ορμών και
συντεταγμένων
του συστήματος.
Οι
εξισώσεις
κίνησης
προκύπτουν από
τις εξισώσεις Hamilton
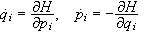 .
.
Αν οι
γενικευμένες
συντεταγμένες
δεν εξαρτώνται
εκπεφρασμένα
από τον χρόνο,
τοτε
H=E, την ολική
ενέργεια του
συστήματος.
Πολλαπλασιαστές
Lagrange
Υποθέστε
ότι για κάποιο
σύστημα
έχετε
επιλέξει
συντεταγμένες
που δεν έναι
ανεξάρτητες
αλλά
συνδέονται
με
m εξισώσεις
δεσμών
της
μορφής
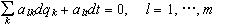 .
.
Τότε
οι εξισώσεις
κίνησης
προκύπτουν
απο
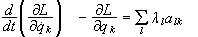 (n εξισωσεις),
(n εξισωσεις),
και
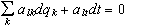 (m εξισώσεις).
(m εξισώσεις).
Έχουμε
m+n εξισώσεις
και m+n αγνώστους,
the n
εξισώσεις και τα m
l.
Οι ll λέγονται πολλαπλασιαστές
Lagrange.
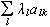 είναι
η γενικευμένη
δυνάμη δεσμών
για
την
γενικευμένη
συντεταγμένη
qk.
είναι
η γενικευμένη
δυνάμη δεσμών
για
την
γενικευμένη
συντεταγμένη
qk.
Μικρές
Ταλαντώσεις
Έστω
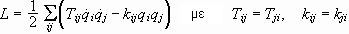 .
.
Τότε
μπορουν να
βρεθουν λύσεις
της μορφής qj
= Re(Ajeiw t). Μπορούμε
να βρουμε το w2
από
την σχέση
det(kij-w 2Tij)=0. Για
ένα σύστημα με n
βαθμούς
ελευθερίας,
μπορούν
να βρεθούν n χαρακτηριστικές
συχνότητες wa .
Ορισμένες
συχνότητες
μπορουν να
είναι
εκφυλισμένες (πολλαπλες
λύσεις).
Φια
συγκεκριμενη
συχνότητα
wa
λύνουμε
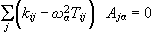
για να
βρούμε τα
Aja . Η
πιο γενική λύση
για κάθε
συντεταγμένη qj είναι
ένα αθροισμα
απλών
αρμονικών
κινήσεων με τις
συχνότητες
wa
.
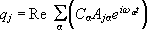 .
.
Κίνηση
Στερεού
Σώματος
Ένα
στερεό
σώμα
είναι ένα
σύστημα
σωματιδίων
στο οποίο
οι αποστάσεις
μεταξύ
των σωματιδίων
παραμένουν
σταθερές. Για
να
περιγράψουμε
την κίνηση
στερεού
σώματος
χρησιμοποιούμε
δύο συστήματα
συντεταγμένων,
ένα σύστημα
X,
Y,
Z, σταθερό στο
χώρο και ένα
κινούμενο
σύστημα
x,
y,
z, που είναι
σταθερά
στερεωμένο στο
σώμα και
συμμετέχει
στην κίνηση του.
Έστω
ότι η αρχή του
συστήματος x,
y, z
είναι το
κέντρο μάζας (CM)
του σώματος. Ο
προσανατολισμός
των αξόνων του
συστήματος
αυτού σχετικά
με τους αξονες
του σταθερου
στο χώρο
συστήματος
δίνεται από
τρεις
ανεξάρτητες
γωνίες.
Το
διάνυσμα
R έχει ως αρχή
την αρχή του
σταθερου στο
χώρο
συστήματος και
τέλος το κέντρο
μάζας του
σώματος.
Επομένως ένα στερεό
σώμα είναι ένα
σύστημα με 6
βαθμους
ελευθερίας.
Εστω
r η θέση ένός
τυχαίου
σημείου P στο
στερεωμένο
στο σώμα
σύστημα
x,
y, z.
Στο σταθερό στο
χώρο σύστημα το
διάνυσμα θέσης
του είναι r+R,
και η
ταχύτητά του
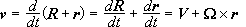 .
.
Όπου
V είναι η
ταχύτητα του
κέντρου μάζας
και W
είναι
η γωνιακή
ταχύτητα του
σώματος. Η
διεύθυνση του W
είναι
κατά μήκος του
άξονα
περιστροφής
και
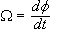 .
.
Η
κινητική
ενέργεια του
σώματος είναι
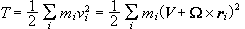 .
.
Έτσι
έχουμε
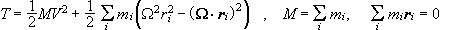 .
.
Βρίσκουμε
λοιπόν
T=
TCM+Trot,
δηλ.
η κινητική
ενέργεια είναι
της κινητικής
ενέργειας του
κέντρου μάζας
συν την
κινητική
ενέργεια
περιστροφής
γύρω από το
κέντρο μάζας.
Για τις
συνιστώσες
έχουμε
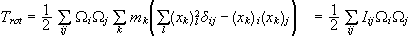 .
.
όπου
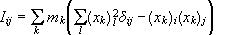
είναι τανυστής
ροπής
αδράνειας. Τα
Wi
είναι
οι συνιστώσες
του
W κατά
μήκος των
αξόνων του
στερεωμένου
στο σώμα
συστήματος. Για
συνεχή
κατανομή μάζας
έχουμε
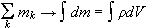 .
.
Με
κατάλληλη
επιλογή της
διεύθυνσης
τους
στερεωμένου
στο σώμα
συστήματος
συντεταγμένων
ο τανυστής
ροπής
αδράνειας
μπορεί να
αναχθεί σε
διαγώνια
μορφή. Οι
διευθύνσεις
των αξόνων xi ονομάζονται
κύριοι
άξονες ροπής
αδράνειας
και
οι διαγώνιες
συνιστώσες του
τανυστή
ονομάζονται
κύριες
ροπές
αδράνειας.
Τότε
έχουμε
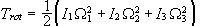 .
.
Ορισμοί:
|
Μη
συμμετρικός
στρόβος:
|
|
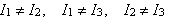
|
|
Συμμετρικός
στρόβος:
|
|
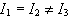
|
|
Σφαιρικός
στρόβος:
|
|
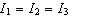
|
Έστω
M η στροφορμή
γύρω
από το κέντρο
μάζας του
σώματος
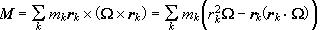 ,
,
η σε
μορφή
συνιστωσών
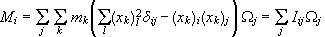 .
.
Αν
x1,
x2,
and x3
είναι
οι κύριοι
άξονες ροπής
αδράνειας,
τότε
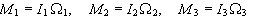 .
.
Η
Lagrangian του στερεού
σώματος είναι
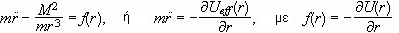 .
.
Οι
εξισώσεις
κίνησης
Οι
εξισώσεις
κίνησης του
στερεού
σώματος είναι
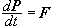 ,
όπου P = ολική
ορμή F
= εξωτερικές
δυνάμεις,
και
,
όπου P = ολική
ορμή F
= εξωτερικές
δυνάμεις,
και
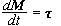 ,
όπου M = στροφορμή
γύρω από κέντρο
μάζας και
t = ολική ροπή από
εξωτερικές
δυνάμεις.
,
όπου M = στροφορμή
γύρω από κέντρο
μάζας και
t = ολική ροπή από
εξωτερικές
δυνάμεις.
Έστω
A τυχαίο
διάνυσμα και
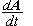 ο
ρυθμός
μεταβολής του
σχετικά με τους
σταθερούς στο
χώρο άξονες,
ο
ρυθμός
μεταβολής του
σχετικά με τους
σταθερούς στο
χώρο άξονες,
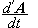 ο
ρυθμός
μεταβολής του
σχετικά με τους
στερεωμένους
στο σώμα άξονες.
Τότε
ο
ρυθμός
μεταβολής του
σχετικά με τους
στερεωμένους
στο σώμα άξονες.
Τότε
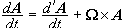 .
.
Επομένως
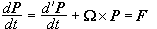 και
και
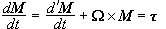 .
.
Έστω
ότι οι
στερεωμένοι
στο σώμα άξονες
είναι οι κύριοι
άξονες ροπής
αδράνειας του
σώματος.
Τοτε
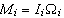 και
και
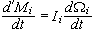
και
έχουμε τις εξισώσεις
του Euler:
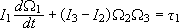
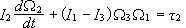
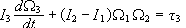
Οι
γωνίες
Euler
Ο
προσανατολισμός
του
στερεωμένου
στο σώμα
συστήματος
συντεταγμένων
ως προς το
σταθερό στο
χώρο σύστημα
συντεταγμένων
περιγράφεται
από τρείς
γωνίες. Αυτές
λέγονται
γωνίες
του
Euler και ορίζονται
στο παρακάτω
σχήμα
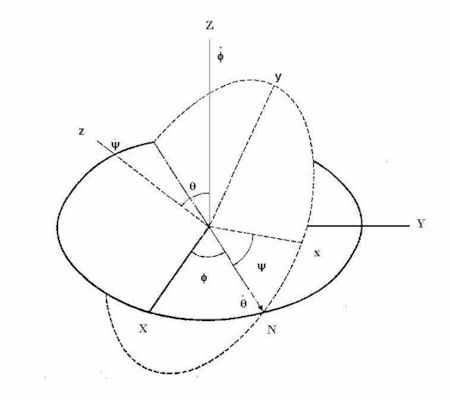
Μπορούμε
να εκφράσουμε
τις συνιστώσες
της γωνιακής
ταχύτητας W κατά
μήκος του
στερεωμένου
στο σώμα
συστήματος x,
y,
z συναρτήσει
των γωνιών Euler και των
παραγώγων τους.
Κίνηση
σε μη αδρανειακό
σύστημα
Έστω
ένα σωμάτιο
κινούμενο με
ταχύτητα v σε σύστημα
συντεταγμένων K
που
κινείται με
ταχύτητα V(t) σχετικά με το
αδρανειακό
σύστημα K0
και
περιστρέφεται
με γωνιακή
ταχύτητα W(t). Η
Lagrangian του σωματίου
είναι
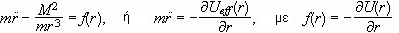 .
.
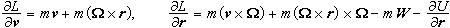 .
.
Οι
εξισώσεις
κίνησης
είναι
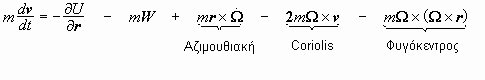
Για
σύστημα
περιστρεφόμενο
με σταθερή
γωνιακή
ταχύτητα
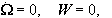 and
the equations
of motion
are
and
the equations
of motion
are
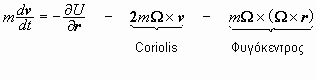
Κίνηση
σε κεντρικό
δυναμικό
Θεωρείστε
ένα σωματίδιο
κινούμενο σε
κεντρικό
δυναμικό.
Σε
κεντρικό
δυναμικό η
ενεργεια Ε και
η στροφορμη M
διατηρούνται. Η κίνηση
γίνεται σε ένα
επίπεδο.
Επιλέγουμε
το επιπεδο αυτό
να είναι το
x-y.
Τότε
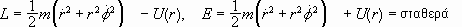 .
.
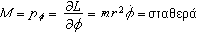 .
.
Δεύτερος
νόμος Kepler:
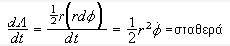 .
.
Η
επιφάνεια που
σαρώνεται στην
μονάδα του
χρόνου είναι
σταθερη για όλα
τα κεντρικά
δυναμικά.
Εξισώσεις
κίνησης που
περιέχουν μόνο
το r:
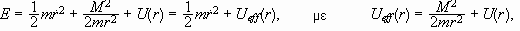
δίνει
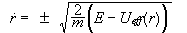 .
.
απο
τις εξισώσεις
Lagrange προκύπτει
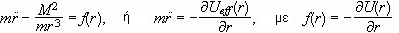 .
.
Εξισώσεις
τροχιάς:
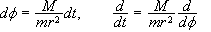 .
.
Απο
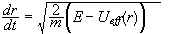
παίρνουμε
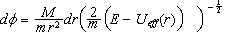 ,
,
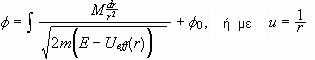 ,
,
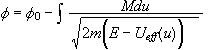 .
.
Απο
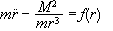
παίρνουμε
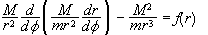 ,
,
ή
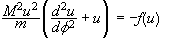 .
.
Το
πρόβλημα Kepler
Έστω
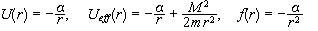 .
.
Η
εξίσωση για την
τροχιά δίνει
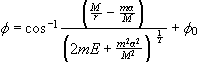 .
.
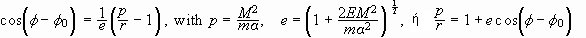 .
.
Αυτή
είναι εξίσωση
κωνικής τομής
ενώ e είναι η εκκεντρότητα.
|
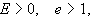
|
|
|
|
υπερβολή
|
|
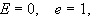
|
|
|
|
παραβολή
|
|
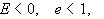
|
|
|
|
έλλειψη
|
|
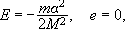
|
|
|
|
κύκλος
|
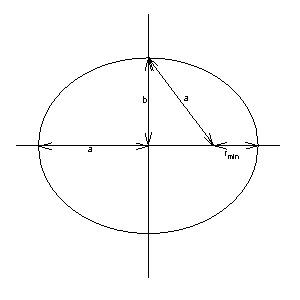
Η
έλλειψη και ο
κύκλος είναι κλειστές
τροχιές. Για
κλειστές
τροχιές έχουμε
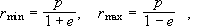
μεγάλος
άξονας:
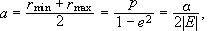
μικρός
άξονας:
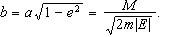
Από
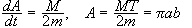
βρίσκουμε
την περίοδο
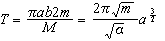 .
.
Αυτός
είναι ο
τρίτος νόμος
του Kepler.
Δύο
αλληλεπιδρώντα
σωματίδια
Στο
σύστημα
κέντρου μάζας
δύο
αλληλεπιδρώντωνσωματιδίων
η Lagrangian
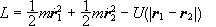
μπορεί
να γραφεί σαν
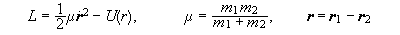 .
.
Το
πρόβλημα των
δυο
αλληλεπιδρώντων
σωματιδίων στο
σύστημα
κέντρου μάζας
τους είναι
ισοδύναμο με το
πρόβλημα ενός
υποθετικού
σωματιδίου ανηγμένης
μάζας m
κινούμενου στο
κεντρικό
δυναμικό U(r).
Ελαστική
Σκέδαση
Θεωρείστε
την
σκέδαση
σωματιδίου απο
κεντρικό
δυναμικό.
Ορίζουμε την
διαφορική
ενεργο διατομή
σκέδασης ως
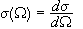
μέσω
της παρακάτω
έκφρασης:
#
σωματιδίων που
σκεδάζονται
στη στερεά
γωνία dΩ στην
μονάδα του
χρόνου=Ι σ(Ω)dΩ ,
όπου Ι
είναι η ένταση
της
προσπίπτουσας
δέσμης δηλαδή
ο αριθμός των
σωματιδίων της
δέσμης ανα
μονάδα
επιφανείας ανα
μοναδα χρόνου.
Για κεντρικά
δυναμικα το σ(Ω)
είναι
ανεξαρτητο της
αζιμουθιακής
γωνίας φ.
Γράφουμε
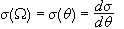 .
.
Ο
αριθμός των
σωματιδίων που
σκεδάζονται
στο γωνιακό
εύρος μεταξυ
θ και θ+dθ ανα
μονάδα χρόνου
είναι
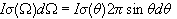 .
.
Ορίζουμε
την παράμετρο
πρόσκρουσης
b απο την σχέση
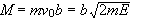 ,
,
όπου M
είναι η
στροφορμή και v0
είναι η
ταχύτητα
προσπτωσης σε
άπειρη
απόσταση.
Όταν τα E και b
καθορισθουν, η
γωνία σκέδασης
είναι
μονοσήμαντα
καθορισμένη
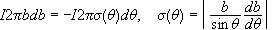 .
.
Σε
κεντρικά
δυναμικα η
κίνηση γίνεται
σε επίπεδο και
τα M και E
είναι σταθερά
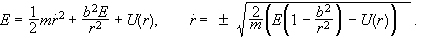
Από
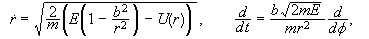
βρίσκουμε
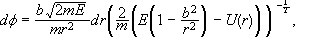
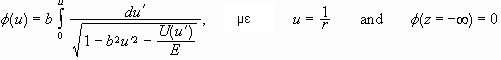 .
.
Έστω θ η
γωνία μεταξυ
της
προσπίπτουσας
και της
σκεδαζόμενης
διεύθυνσης και
φ0 η γωνία
μεταξύ r( z=-~)
και rmin. Τότε
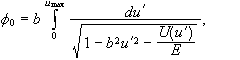
και
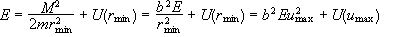
μας
δίνει το umax.
Έχουμε
θ =π-2φ0
για απωστικό
δυναμικό
θ
=2φ0-π
για ελκτικό
δυναμικό (ή θ=π-2φ0,
θ
<
0).
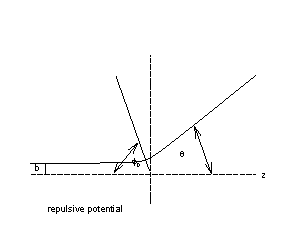
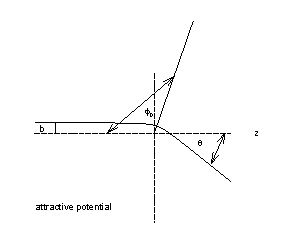
Αν
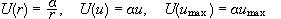
τότε
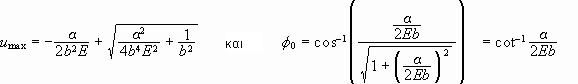 .
.
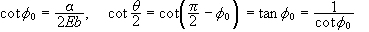 .
.
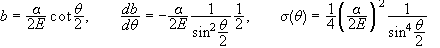
Ενεργός
διατομή Rutherford
Μετασχηματισμοί
Συστημάτων
Αναφοράς
Ο
αριθμός των
σωματιδίων που
σκεδάζονται σε
ανιχνευτή
είναι ο ίδιος
στο σύστημ
εργαστηρίου
και στο σύστημα
κέντρου μάζας.
Επομένως
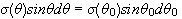 .
.
![]()
![]()
![]()

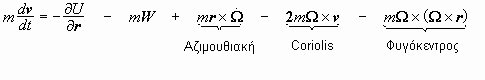
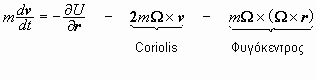
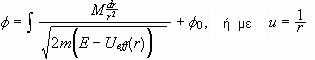 ,
,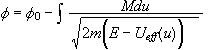 .
.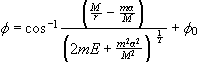 .
.
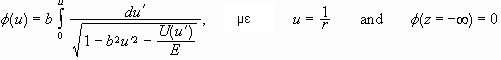 .
.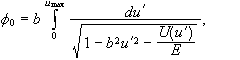


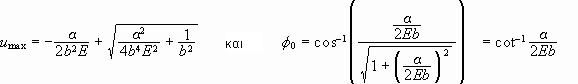 .
.